اختبار T لعينة واحدة

لدينا

x̅ = 54.8

S = 4.3

μ = 57.20

N = 25

نتبع الخطوات التالية:

1- تحديد مستوى الدلالة: α = 0.05.

2- الفروض الإحصائية: الفرضية في هاته الحالة متجهة والاختبار يكون ذو طرف واحد.

الفرضية الصفرية: H₀: x̅ ≥ µ لا توجد فروق بين المتوسط الحسابي للعينة والمتوسط العام لتعليم المبتدئين

الفرضية البديلة: H₁: x̅ < µ يوجد فروق بين المتوسط الحسابي للعينة والمتوسط العام لتعليم المبتدئين لصالح العينة

3- حساب قيمة T المحسوبة:

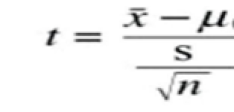
= (54.8 – 57.20) ÷ ( 4.3 ÷ 25√) = -2.4 ÷ 0.86 = - 2.79

تهمل الإشارة السالبة (الإشارة لا تهم في اختبار T)

T = 2.79

4- حساب قيمة T الجدولية بالطريقة التالية:

- مستوى الدلالة α = 0.05

- حساب درجة الحرية = ن - 1 = 25 - 1 = 24

من خلال القيم الجدولية لاختبار T نلاحظ أن قيمة تقاطع α مع درجة الحرية هي T الجدولية وتساوي: 1.711

5- القرار الإحصائي:

نلاحظ أن قيمة T المحسوبة أكبر من T الجدولية أي 2.79 > 1.711 وبالتالي نرفض الفرض الصفري الذي يقر أن متوسط العينة مساوي لمتوسط المجتمع ونقبل الفرض البديل أي توجد فروق ذات دلالة إحصائية بين متوسط العينة ومتوسط المجتمع لصالح العينة وبالتالي فالطريقة الجديدة جعلت عملية التعلم أسرع.