اختبار T لعينة واحدة

لدينا

x̅ = 47.84

S = 5.66

N = 10

حساب المتوسط الفرضي μ

المتوسط الفرضي = (مجموع درجات البدائل ÷ عدد البدائل) × عدد عبارات المقياس

لدينا 3 بدائل كل بديل له درجة تعطى تدريجيا بشكل مرتب

البديل الأول درجته 1، البديل الثاني درجته 2، البديل الثالث درجته 3.

إذن مجموع البدائل = 1 + 2 + 3 = 6، عدد البدائل = 3، عدد عبارات المقياس = 20

المتوسط الفرضي = (6 ÷ 3) × 20 = 2 × 20 = 40

وبالتالي μ = 40.

لمعرفة دلالة الفروق نتبع الخطوات التالية:

1- تحديد مستوى الدلالة: α = 0.05.

2- الفروض الإحصائية: الفرضية غير متجهة إذن الاختبار ذو طرفين

الفرضية الصفرية: H₀: x̅ = µ لا توجد فروق بين المتوسط الحسابي للعينة والمتوسط الفرضي للمقياس

الفرضية البديلة: H₁: x̅ ≠ µ يوجد فروق بين المتوسط الحسابي للعينة والمتوسط الفرضي للمقياس.

3- حساب قيمة T المحسوبة:

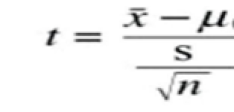
= (47.84 – 40) / (5.66 ÷10√) = 7.84 / 1.79 = 4.38

T = 4.38

4- حساب قيمة T الجدولية بالطريقة التالية:

- مستوى الدلالة α = 0.05

- حساب درجة الحرية = ن - 1 = 10- 1 = 9

من خلال القيم الجدولية لاختبار T نلاحظ أن قيمة تقاطع α مع درجة الحرية هي T الجدولية وتساوي: 2.26

5- القرار الإحصائي:

نلاحظ أن قيمة T المحسوبة أكبر من T الجدولية أي 4.38 > 2.26 وعليه نرفض الفرض الصفري ونقبل الفرض البديل الذي ينص على وجود إحصائية فروق ذات دلالة إحصائية بين متوسط العينة والمتوسط الفرضي للمقياس ولصالح متوسط العينة (لأن متوسط العينة أكبر من المتوسط الفرضي)، ومن هنا نستنتج أن مستوى اتجاهات العينة نحو التخصص هو مستوى عالي.