اختبار ت لعينتين مستقلتين

لاختبار دلالة الفروق بين متوسطي عينتين نتبع الخطوات التالية:

1- تحديد مستوى الدلالة: والتي غالبا ما تكون قيمتها (α = 0.05) وأحيانا (α = 0.01)

2- تحديد الفروض الإحصائية:

وذلك بافتراض أن x̅₁ تساوي قيمة x̅₂ ويمكن تمثيل ذلك كالآتي:

الفرضية الصفرية: H₀: x̅₁ = x̅₂ لا توجد فروق بين متوسطي العينتين.

الفرضية البديلة: H₁: x̅₁ ≠ x̅₂ توجد فروق بين متوسطي العينتين.

3- حساب قيمة ت المحسوبة.

4- حساب قيمة Tت الجدولية بالطريقة التالية:

- تحديد مستوى الدلالة.

- حساب درجة الحرية بحيث:

* إذا كانت العينتين غير متساويتين فدرجة الحرية = ن₁ + ن₂ - 2

* إذا كانت العينتين متساويتين فدرجة الحرية = 2ن - 2

- استخراج ت الجدولية من جدول Ttest وهي القيمة التي تتقاطع فيها درجة الحرية مع مستوى الدلالة.

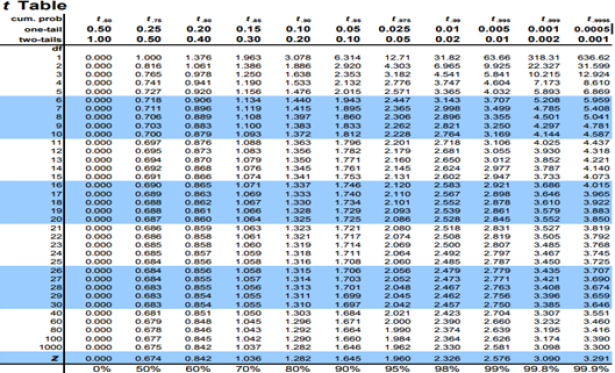
5- إتخاذ القرار: وذلك بمقارنة قيمة ت المحسوبة مع قيمة ت الجدولية بحيث:

- إذا كانت ت المحسوبة أصغر من ت الجدولية نقبل الفرض الصفري الذي ينص على عدم وجود فروق بين متوسطي العينتين.

- إذا كانت ت المحسوبة أكبر أو يساوي ت الجدولية نرفض الفرض الصفري ونقبل الفرض البديل الذي ينص على أنه توجد فروق ذات دلالة إحصائية بين متوسطي العينتين ولصالح العينة التي لها أحسن متوسط حسابي.