6- حل التمرين:
1- تحديد مستوى الدلالة:
α = 0.05
2- تحديد الفروض الإحصائية:
H0: x̅1 = x̅2 لا توجد فروق ذات دلالة إحصائية بين القياس القبلي والقياس البعدي في متغير قلق المنافسة.
H1: x̅1 ≠ x̅2 توجد فروق ذات دلالة إحصائية بين القياس القبلي والقياس البعدي في متغير قلق المنافسة.
3- حساب قيمة ت المحسوبة:
وذلك بتطبيق القانون التالي:

نضع الجدول التالي لتسهيل الحساب:
الأفراد | القياس القبلي | القياس العدي | ف | ف2 |
1 | 18 | 16 | 2 | 4 |
2 | 19 | 16 | 3 | 9 |
3 | 17 | 18 | -1 | 1 |
4 | 15 | 15 | 0 | 0 |
5 | 19 | 17 | 2 | 4 |
6 | 20 | 18 | 2 | 4 |
7 | 22 | 21 | 1 | 1 |
8 | 20 | 21 | -1 | 1 |
9 | 17 | 14 | 3 | 9 |
10 | 17 | 16 | 1 | 1 |
المجموع | ̅س1 = 18.4 | ̅س2 = 17.2 | 12 | 34 |
بالتعويض في المعادلة:
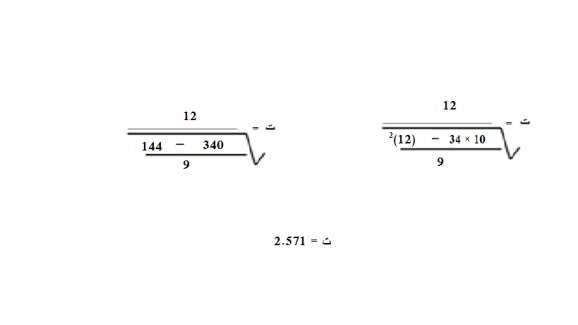
4- حساب قيمة ت الجدولية بالطريقة التالية:
- تحديد مستوى الدلالة: 0.05
- حساب درجة الحرية وتساوي ن - 1 = 9
- استخراج ت الجدولية من جدول Ttest وهي القيمة التي تتقاطع فيها درجة الحرية مع مستوى الدلالة.
إذن ت الجدولية = 2.26
5- القرار الإحصائي:
بما أن ت المحسوبة > ت الجدولية أي: 2.571 > 2.26 إذن نرفض الفرض الصفري ونقبل الفرض البديل الذي يقرر أن تناول العقار المهدئ يخفض قلق المنافسة لدى أفراد العينة
وبالتالي توجد فروق ذات دلالة إحصائية بين القياس القبلي والقياس البعدي ولصالح القياس البعدي.
ملاحظة :
كيف عرفنا أن النتيجة لصالح القياس البعدي:
لإن القياس البعدي هو من لديه أحسن متوسط حسابي
ففي بعض المقاييس والاختبارات كلما زاد المتوسط كانت النتيجة أحسن مثل مقياس الثقة بالنفس واختبار رمي كرة طبية.
وفي بعض المقاييس والاختبارات كلما نقص المتوسط الحسابي كانت النتيجة أحسن مثل مقاييس القلق واختبارات السرعة.